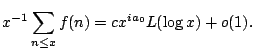Let
Let ![]() denote the
number of primes not exceeding the real number
denote the
number of primes not exceeding the real number ![]() . In 1793 C.F. Gauß [7] and in 1798 A.M Legendre [19] proposed independently that for
large
. In 1793 C.F. Gauß [7] and in 1798 A.M Legendre [19] proposed independently that for
large ![]() the ratio
the ratio
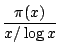
In 1851 the russian mathematician P.L. Chebychev [1] made an important step forward by
proving that if the ratio did tend to a limit, then this limit must be
one. Further, he succeeded in showing that the actual order of ![]() is
is ![]() , that is
, that is
In 1859 B. Riemann [20] attacked the problem with analytic methods, using a formula discovered by L. Euler in 1737 which relates the prime numbers to the function
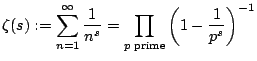
Thirty years later the necessary analytic tools were at hand and in 1896 J. Hadamard [9] and C.J de la Vallée Poussin [23] independently and almost simultaneously succeeded in proving that
This remarkable result is called the prime number
theorem, and its proof was one of the crowning achievements of
analytic number theory.
The prime number theorem was subsequently reproved and improved by
others. However, a proof of this theorem, not fundamentally dependent
upon the ideas of the theory of functions, seemed, not only to G.H.
Hardy (cf. [11] p.549-550),
extraordinarily unlikely. In his talk on "Goldbach`s Theorem" given for
the Mathematical Society in Kopenhagen on October 6, 1921 he says:
"...Let us turn back ...to its central theorem,
the `Primzahlsatz` or `prime number theorem`...No elementary proof is
known, and one may ask whether it is reasonable to expect one. Now we
know, that the theorem is roughly equivalent to a theorem about an
analytic function, the theorem that Riemann`s Zeta-function has no
zeros on a certain line. A proof of such a theorem, not fundamentally
dependent upon the ideas of the theory of function, seems to me
extraordinarily unlikely. It is rash to assert that a mathematical
theorem cannot be proved in a particular way ...If anyone produces an
elementary proof of prime number theorem, he will show that these views
are wrong, that the subject does not hang together in the way we have
supposed ..."
Therefore, in 1949 A. Selberg [21]
and P. Erdös [4] caused a sensation
when they discovered an elementary proof of the prime number theorem.
Their proof, though very intricate, makes no use of ![]() nor of complex function theory and in principal is
accessible to anyone familiar with elementary analysis.
nor of complex function theory and in principal is
accessible to anyone familiar with elementary analysis.
In 1911 E. Landau [18] showed that
the prime number theorem is equivalent to the validity of the assertion
that the mean value ![]() of the Möbius function
of the Möbius function ![]() exists and is equal to zero.
We say that the function
exists and is equal to zero.
We say that the function ![]() possesses a mean value
possesses a mean value
![]() if the limit
if the limit
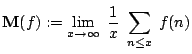
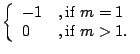 |
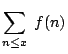 could be fully determined for all
complex-valued multiplicative functions
could be fully determined for all
complex-valued multiplicative functions
Proposition (Halász's theorem). Let
![]() be multiplicative,
be multiplicative,
![]() If there
exists a real number
If there
exists a real number ![]() so that the series
so that the series
converges for ![]() , then, as
, then, as
![]() ,
,
If the series (1) diverges for all
![]() , then
, then
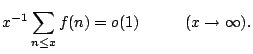
![]() and a slowly oscillating function
and a slowly oscillating function ![]() with
with ![]() , so that, as
, so that, as
![]()