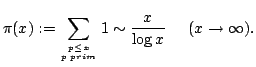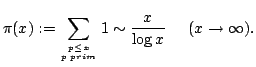Seminar Funktionentheorie/Zahlentheorie

Prof. Dr. Indlekofer

Organisatorisches

Seminar Funktionentheorie/Zahlentheorie:
- Donnerstag, 11 - 13 Uhr, N2.228

In diesem Seminar sind die folgenden Themen vorgesehen:

Thema 1: Elementarer Beweis des Primzahlsatzes
(bis zu 2 Vorträge)
Thema 2: Die Formel von Perron und Anwendung für analytischen Beweis des Primzahlsatzes
(bis zu 3 Vorträge)
Thema 3: Die Sätze von Wintner und Axer
(bis zu 2 Vorträge)

Interessenten können sich ab sofort bei Laszlo German (E-Mail: laszlo@math.upb.de) melden.

Thema 1: Elementarer Beweis des Primzahlsatzes

Wie zufällig sind Primzahlen? Sie wachsen unter den natürlichen Zahlen wie Unkraut, genügen aber andererseits einem festen Gesetz, dem Primzahlsatz

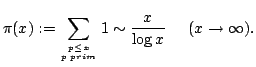
$\displaystyle \pi(x):=\sum_{p \leq x \atop p \; prim} 1 \sim \frac{x}{\log x} \;\;\;\;\; (x \to \infty).$

Der Elementare Beweis des Primzahlsatzes ist ein Beweis, der keine höheren Kenntnisse außer der elementaren Ergebnisse der Analysis einer Veränderlichen benötigt. Hier sollen einige Elementare Beweise des Primzahlsatzes veranschaulicht werden.

Weiterführende Literatur

Specht, W.: Elementare Beweise der Primzahlsätze, Berlin, Deutscher Verlag der Wissenschaften, 1956
Hardy, G.H. und E.M. Wright: Einführung in die Zahlentheorie. R. Oldenburg, München, 1958.

Thema 2: Die Formel von Perron und Anwendung für funktionentheoretischen Beweis des Primzahlsatzes

Zum Vergleich der Komplexität der Methode, die in Thema 1. angewendet wird, diskutieren wir eine funktionentheoretische Annäherung, die einfacher ist.
Die Formel von Perron erlaubt es, von den Eigenschaften einer durch Dirichletschen Reihe gegebenen Funktion

$\begin{displaymath} f(s):=\sum_{n}a_n n^{-s} \end{displaymath}$

auf die Größe der Koeffizientensumme

$\begin{displaymath} \sum_{n\leq x} a_n \end{displaymath}$

zurückzuschließen. Durch die Anwendung dieser Formel, beweisen wir den Primzahlsatz.

Weiterführende Literatur

Prachar, K.: Primzahlverteilung. Springer-Verlag 1957.
Apostol, T.M.: Introduction to Analytic Number Theory, Springer-Verlag, 1976.

Thema 3: Die Sätze von Wintner und Axer

Die Menge A der zahlentheoretischen Funktionen bildet mit der Addition + und der Dirichletschen Faltung * einen Ring (A,+,*), von dem man zeigen kann, dass es sich um einen ZPE-Ring handelt. Einfache Inversionsformeln bilden die Grundlage bei der Untersuchung des Primzahlsatzes und für das Summationsverhalten arithmetischer Funktionen. Beispielhaft werden die Sätze von Wintner und Axer bewiesen.

Weiterführende Literatur

Axer, A.: Beitrag zur Kenntnis der zahlentheoretischen Funktionen μ(n) und λ(n). Prace math.-fiz. 21 (1910), 65-95.
Schwarz, W. und J. Spilker: Arithmetical Functions. Cambridge University Press, Cambridge, 1994.
Wintner, A.: Eratosthenian Averages. Waverly, Baltimore 1943.

Hier können Sie Ihre eigene Literaturrecherche in der Bibliothek durchführen.