Seminar für Lehramtskandidaten
Seminar Funktionentheorie/Zahlentheorie

Prof. Dr. Indlekofer
Organisatorisches
- Seminar für Lehramtskandidaten:
- Dienstag, 11 - 13 Uhr, J2.331
- Seminar Funktionentheorie/Zahlentheorie:
- Donnerstag, 11 - 13 Uhr, N2.228
In diesen Seminaren sind die folgenden Themen vorgesehen:
Interessenten können sich ab sofort melden bei Frau Anna Barat (Tel: 602601, E-Mail: bam10@math.upb.de).
Die älteste uns überlieferte Form, eine Nachricht zu verschlüsseln, ist wohl die der Spartaner, mit der sie schon im fünften Jahrhundert vor unserer Zeitrechnung "chiffriert" haben:
Es wurde ein Papierstreifen spiralförmig um einen Stab, die Skytala, gewickelt. Die parallel zum Stab auf dem Papierstreifen geschriebene Information erschien sinnlos, wenn der Papierstreifen abgenommen wurde. Wurde der Papierstreifen jedoch an seinem Bestimmungsort auf einem Stab des gleichen Durchmessers gewickelt, so konnte die "verschlüsselte" Information leicht entziffert werden.
Zentraler Punkt dieses Vortrags ist das RSA-Verfahren, das auf Ideen von Diffie und Hellmann aus dem Jahr 1976 zurückgeht und dessen effektive Implementierung 1978 von Rivest, Shamir und Adleman vorgeschlagen wurde.
Weiterführende Literatur
- Buchmann, J.: Einführung in die Kryptographie. Springer-Verlag 2004.
- Kranakis, E.: Primality and Cryptograhy. Teubner and
John Wiley 1986.
- Ribenboim, P.: The New Book of Prime Numer Records. Springer, 1996.
Ähnlich wie das Guiness-Buch der Rekorde hat sich für den Bereich der Primzahlen The New Book of Prime Numer Records von Ribenboim als maßgebliche Informationsquelle etabliert. Aus der Fülle der Fragestellungen greifen wir heraus
- Wie viele Primzahlen gibt es?
- Wie erkennt man, dass eine natürliche Zahl prim ist?
- Heuristische und probabilistische Ergebnisse über Primzahlen.
Weiterführende Literatur
- Buchmann, J.: Einführung in die Kryptographie. Springer-Verlag 2004.
- Kranakis, E.: Primality and Cryptograhy. Teubner and
John Wiley 1986.
- Ribenboim, P.: The New Book of Prime Number Records. Springer, 1996.
Wie zufällig sind Primzahlen? Sie wachsen unter den natürlichen Zahlen wie Unkraut, genügen aber andererseits einem festen Gesetz, dem Primzahlsatz
Welche Struktur der natürlichen Zahlen bewirkt dieses geordnete Verhalten? Ist es die Eigenschaft, dass
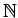 bezüglich der Multiplikation oder, wenn wir die Null hinzunehmen, bezüglich der Addition eine Halbgruppe bildet? Wir werden die Antwort finden.
bezüglich der Multiplikation oder, wenn wir die Null hinzunehmen, bezüglich der Addition eine Halbgruppe bildet? Wir werden die Antwort finden.
Weiterführende Literatur
- Knopfmacher, J.: Abstracht Analytic Number Theory.
North-Holland Publ. Co., Amsterdam, 1975, Second Edition, Dover Publ., New
York 1996.
- Knopfmacher, J.: Analytic arithmetic of algebraic
function fields. Lecture Notes in Pure ans Applied Mathematics, Vol. 50,
Marcel Dekker, New York, Basel, 1979.
- Knopfmacher, J. and W.B. Zhang: Number Theory arising
from Finite Fields. Marcel Dekker, New York, Basel, 2001.
- Barat, A.: Prime number theorems in additive
arithmetical semigroups. Diplomarbeit, Paderborn, 2004.
Die Ungleichungen des Großen Siebes sind allgegenwärtig in der heutigen analytischen Zahlentheorie. In seiner modernen Formulierung handelt es sich dabei um kein Siebverfahren im zahlentheoretischen Sinn, sondern um eine Ungleichung zwischen verschiedenen Mittelwerten eines trigonometrischen Polynoms. Nach einigen elementaren Untersuchungen über die Eigenwerte gewisser hermetischer Matrizen zeigen wir: Das Große Sieb ist ein Sieb!
Weiterführende Literatur
- Elliott, P.D.T.A.: Probabilistic Number Theory I.
Springer 1979.
- Montgomery, H.L.: Topics in Multiplicative Number
Theory. Springer, 1971.
- Montgomery, H.L.: Hilbert's inequality and the Large
Sieve. Proceedings at the Number Theory Conference Boulder (1972),
156-161.
Die Menge A der zahlentheoretischen Funktionen bildet mit der Addition + und der Dirichletschen Faltung * einen Ring (A,+,*), von dem man zeigen kann, dass es sich um einen ZPE-Ring handelt. Einfache Inversionsformeln bilden die Grundlage bei der Untersuchung des Primzahlsatzes und für das Summationsverhalten arithmetischer Funktionen.
Weiterführende Literatur
- Axer, A.: Beitrag zur Kenntnis der zahlentheoretischen
Funktionen μ(n) und λ(n). Prace math.-fiz. 21 (1910),
65-95.
- Lucht, L.G.: Die Sätze von Wintner und Axer.
Clausthal-Zellerfeld, 2006.
- Schwarz, W. und J. Spilker: Arithmetical Functions.
Cambridge University Press, Cambridge, 1994.
- Wintner, A.: Eratosthenian Averages. Waverly,
Baltimore 1943.
Die Menge A der zahlentheoretischen Funktionen bildet mit der Addition + und der Dirichletschen Faltung * einen Ring (A,+,*), von dem man zeigen kann, dass es sich um einen ZPE-Ring handelt. Einfache Inversionsformeln bilden die Grundlage bei der Untersuchung des Primzahlsatzes und für das Summationsverhalten arithmetischer Funktionen. Beispielhaft werden die Sätze von Wintner und Axer bewiesen.
Weiterführende Literatur
- Axer, A.: Beitrag zur Kenntnis der zahlentheoretischen
Funktionen μ(n) und λ(n). Prace math.-fiz. 21 (1910),
65-95.
- Lucht, L.G.: Die Sätze von Wintner und Axer.
Clausthal-Zellerfeld, 2006.
- Schwarz, W. und J. Spilker: Arithmetical Functions.
Cambridge University Press, Cambridge, 1994.
- Wintner, A.: Eratosthenian Averages. Waverly,
Baltimore 1943.
Unter einer Partition einer natürlichen Zahl n verstehen wir eine Darstellung der Form
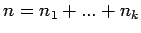 mit Summanden
mit Summanden
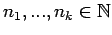 Partition von n, die durch eine Permutation der Summanden auseinander hervorgehen, werden nicht unterschieden. Es werden Rekursionen für die Anzahl der Partitionen von natürlichen Zahlen einschließlich des Pentagonalzahlensatzes von Euler und Legendre bewiesen.
Partition von n, die durch eine Permutation der Summanden auseinander hervorgehen, werden nicht unterschieden. Es werden Rekursionen für die Anzahl der Partitionen von natürlichen Zahlen einschließlich des Pentagonalzahlensatzes von Euler und Legendre bewiesen.
Weiterführende Literatur
- Hardy, G.H. und E.M. Wright: Einführung in die
Zahlentheorie. R. Oldenburg, München, 1958.
- Lucht, L.G.: Einführung in die Zahlentheorie.
Vorlesungsausarbeitung, TU Clausthal, WS 2005/2006.
- Lucht, L.G.: Partitionen. Clausthal-Zellerfeld, 2006.
Das Dirichletsche Schubfachprinzip liefert eine elementare Aussage über die Güte der Approximation von reellen Zahlen durch rationale Zahlen. Ein 1844 von Liuoville bewiesener Satz verbindet die Güte rationaler Approximation mit der Ordnung von algebraischen Zahlen und ermöglicht die Konstruktion von transzendenten Zahlen. Der Begriff der besten Approximation führt auf den Kettenbruchalgorithmus.
Weiterführende Literatur
- Baker, A.: Transcendental Number Theory. Cambridge
Univ. Press, Cambridge, 1975.
- Cassels, J.W.S: An Introduction to Diophantine
Approximation. Cambridge Univ. Press, London, 1965.
- Lucht, L.G.: Rationale Approximation reeller Zahlen.
Clausthal-Zellerfeld, 2006.
- Hardy, G.H. und E.M. Wright: Einführung in die
Zahlentheorie. R. Oldenburg, München, 1958.
- Le Vesque, W.J.: Fundamentals of Number Theory.
Reprint, Dover Publ., New York, 1996.
Liouville zeigte 1844 die Existenz transzendenter Zahlen konstruktiv. Ein reiner Existenzbeweis geht auf Cantor 1874 zurück. Der Nachweis der Transzendenz gegebener Zahlen ist schwieriger. Hier wird die von Hermite 1873 und von Lindemann 1882 bewiesene Transzendenz der Zahlen e und π gezeigt.
Weiterführende Literatur
- Baker, A.: Transcendental Number Theory. Cambridge
Univ. Press, Cambridge, 1975.
- Hardy, G.H. und E.M. Wright: Einführung in die
Zahlentheorie. R. Oldenburg, München, 1958.
- Hornfeck, B.: Algebra. de Gruyter, Berlin, 1969.
- Lucht, L.G.: Die Tanszendenz von e und π.
Clausthal-Zellerfeld, 2004.
- Siegel, C.L.: Transzendente Zahlen. BI, Mannheim,
1967.
Ein klassisches Ergebnis von Abel (1826) besagt
Sei die Potenzreihe
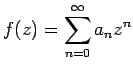 konvergent für
konvergent für 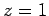 . Dann gilt
. Dann gilt
Dieses Resultat ist ein Prototyp aus der Klasse von sog. Abelschen Sätzen, die dadurch charakterisiert sind, dass, falls eine Folge (oder eine Funktion) genügend "regulär" ist, auch bestimmte gemittelte Werte ein reguläres Verhalten zeigen.
Beispielsweise ist auch
ein Abelscher Satz. Die Umkehrung eines Abelschen Satzes ist i.a. falsch, wie etwa das Beispiel
für z→ 1 zeigt:
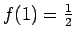
, aber
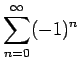
konvergiert nicht.
Weiterführende Literatur
- van Aaardenne-Ehrenfest, T./ de Bruijn, N.G./ und Korevaar,
I.: A note on slowly oscillating functions. Nieuw. Arch. Wiskunde
23 (1949), 77-86.
- Hardy, G.H. und J.E. Littlewood: Tauberian theorems
concerning power series and Dirichlet`s series whose coefficients are
positive. Proc. London Math. Soc. 13, (1914),174-191.
- Hardy, G.H. : Divergent Series. Oxford University
Press, London 1949.
- Karamata, J.: Sur une mode de croissance reguliere
de fonctions}. Math. (Cluj) 4 (1930), 38-53.
- Karamata, J.: Neuer Beweis und Verallgemeinerung der
Tauberschen Sätze, welche die Laplacesche Transformation bertreffen.
Math.Z. 164 (1931), 319-320.
- Kohlbecker, E.E.: Weak asymptotic properties of
partitions. Trans. Am. Math. Soc. 88 (1958), 346-365.
- Korevaar, J.: Tauberian Theory, a Century of
Developments. Springer, Berlin, 2004.
- Lucht, L.G.: Slowly Oscillating Functions and Tauberian
Theorems. Clausthal-Zellerfeld, 2005.
- Seneta, E.: Regularly varying functions. Lecture Notes
in Mathematics 508, Springer-Verlag, Berlin-Heidelberg-New York, 1976.
- Tauber, A.: Ein Satz aus der Theorie der unendlichen
Reihen. Monatsh. Math. u. Phys. 8 (1897), 273-277.
- Wirsing, E.: Das asymptotische Verhalten von Summen
über multiplikative Funktionen. Math. Ann. 143 (1961), 75-102.
- Wirsing, E.: The asymptotic behaviour of sums of
multiplicative functions. Lecture Notes, ed. I. Anderson, University of
Nottinham, Department of Mathematics, 1967.
- Wirsing, E.: The asymptotic behaviour of sums of
multiplicative functions II. Acta. math. Hungar. 18 (1967), 414-467.
Hier können Sie Ihre eigene Literaturrecherche in der
Bibliothek durchführen.
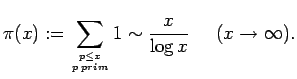
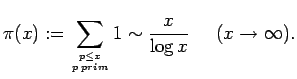
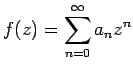 konvergent für
konvergent für ![]() . Dann gilt
. Dann gilt
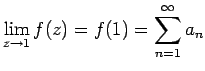
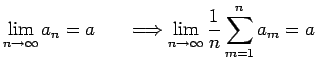
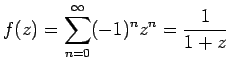
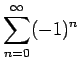 konvergiert nicht.
konvergiert nicht.